べき乗則の背後に同期現象の存在―ある普遍的現象が別の普遍的現象を誘発―
- ヘッドライン
- 記者発表
東京大学
発表のポイント
◆生態系をはじめとしてさまざまな分野で成立が確認されている別々の普遍的な現象「Taylor's law(TL)」と「同期現象」において、TLが同期現象によって誘発される可能性があることを示しました。
◆TLの発生機構の一つに同期現象があり得ることを数値的・解析的に示しました。
◆TLの存在から同期状態を検出できる可能性があり、また、心臓や通信網などの強く結合したシステムに共通する普遍的な性質の理解につながることが期待されます。
発表概要
東京大学大学院新領域創成科学研究科の三井 譲大学院生(研究当時、現:九州大学助教)と郡宏教授らによる研究グループは、Taylor's law(以下TLと略記)と呼ばれる平均と分散の間に成立するべき乗則(注1)が、同期現象(注2)によって誘発される可能性があることを数理モデルによって示しました。
TLは、さまざまな分野でその成立が観測されている普遍的な法則であり、特に生態系における生物の個体数変動データにおいて幅広く観測されてきました。また、TLの指数は生物分布の推定に用いられることがあり、生態系において観測されるTLの指数(注3)に2が多いことが分かっています。しかしながら、どのような仕組みでこの普遍的なべき乗則が成立しているのかは明らかになっていませんでした。
本研究では、TLと同様に生態系で幅広く観測されている現象である、同期現象に着目しました。同期現象もまた、さまざまな分野で観測されている普遍的な現象です。同期現象を再現できる数理モデルを用いた解析の結果、同期現象を起こすとそれに伴ってTLが現れるということが分かりました(図1)。特に、数理モデルに強い結合を与えることにより時系列が互いに定数倍の関係になるような同期状態が発生し、指数が2であるTLが現れることが分かりました。
この結果はさまざまな数理モデルで再現されることが分かり、TLの存在から逆に同期状態を推定できる可能性が示唆されました。今後、心臓や次世代通信などの強い結合が必要とされるシステムにおける普遍的な性質の一端の理解に役立つことが期待されます。
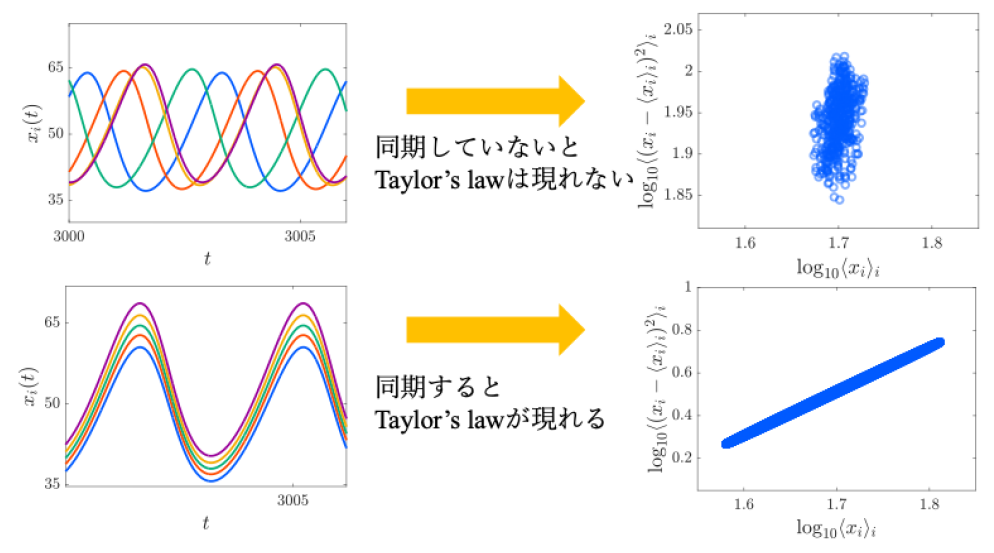
図1:同期現象に誘発されるTaylor's law
同期していない時系列データから平均と分散の関係を計算してもTLは観測されない(上段)が、同期している時系列データからはTLが観測される(下段)。
発表内容
【研究背景】
Taylor's law(以下TLと略記)とは平均と分散の間に成立するべき乗則のことであり、生態学を中心にさまざまな分野でその成立が確認されている普遍的な法則です。生態学においては、自然界における生物の個体数変動データを用いてこの法則が広範に確認されており、TLの指数は生物がどのように分布しているのかを推論するのに用いられることがあります。しかしながら、どのような仕組みでこの普遍的なべき乗則が成立しているのかについては詳細が明らかになっていませんでした。特に、いろいろな分野がある中でとりわけ生態学において幅広くTLの成立が観測されているのはなぜなのか、生態系において観測されるTLの指数に2が多いのはなぜなのかといった問題が残されていました。
【研究成果】
本研究では、TLと同様に生態学において広く観測されている現象である同期現象に着目しました。同期現象もまた、生態学以外においても、さまざまな分野で確認されている普遍的な現象です。生態系における同期現象とは、離れた場所に生息している生物の個体数の増減タイミングが一致する現象のことです。もしTLの背後に同期現象の存在があることが言えたならば、生態系において広範にTLが観測されていることに対する説明がつけられるのではないかと考え研究をスタートしました。本研究では、生態系における同期現象を再現することができる数理モデルを用いてこの問題にアプローチしました。数理モデルを用いたシミュレーションを行なってみると、同期現象が起きていないときにはTLが観測されないが、同期現象が起きているときにはTLが観測されるということが確認できました(図2)。特に、数理モデルに強い結合を与えると、時系列同士が互いに定数倍の関係になるような同期状態(この状態をwaveform proportionalityと名付けました)が発生し、その結果として指数2のTLが現れるということが分かりました(図2下段)。数理モデルを記述する微分方程式(注4)を近似的に解き、これらの結果を解析的に説明することもできました。さらに、これらの結果はさまざまな数理モデルで再現されることも分かりました。
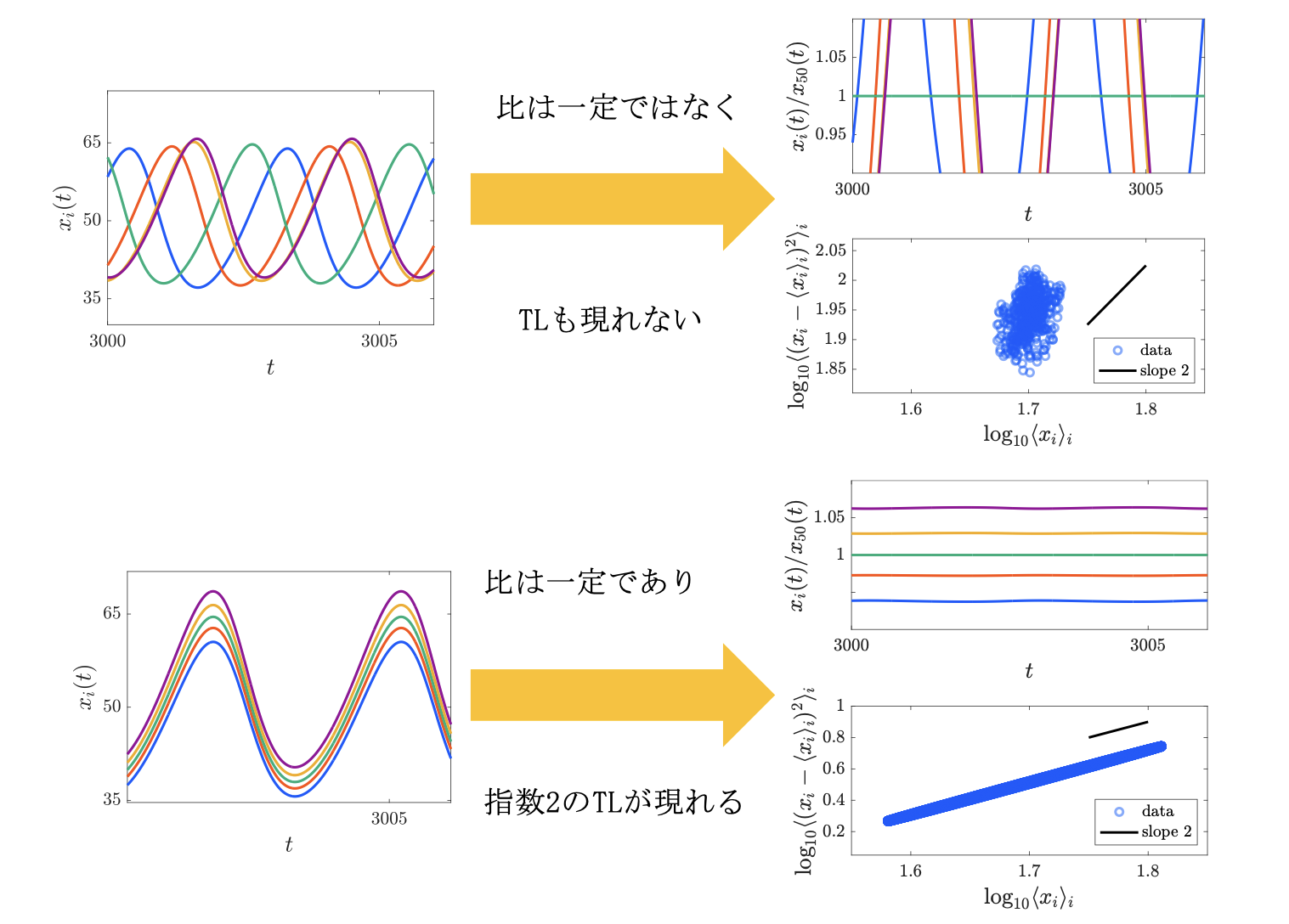
図2:同期現象に誘発されるwaveform proportionalityと指数2のTL
(上段)非同期状態では時系列同士の比は一定でなくTLも現れない。(下段)強い結合による同期状態では時系列の比が一定(waveform proportionality)になり、指数2のTLが現れる。
※2025年5月7日、図2を差し替えました。
【研究の意義・今後の展望】
本研究では指数2のTLと同期現象の関係を数値的・解析的に結びつけることに成功しました。この結果を利用して、指数2のTLを同期現象の検出に用いることができるのではないかと考えています。また、心臓や次世代通信などのような、安定した駆動のために強い結合が必要になるシステムの普遍的な性質の理解にも役立つことが期待されます。
発表者・研究者等情報
東京大学大学院新領域創成科学研究科
三井 譲 博士課程/日本学術振興会特別研究員(研究当時)
現:九州大学 芸術工学研究院 助教
郡 宏 教授
論文情報
雑誌名:Physical Review Letters
題 名:Waveform proportionality and Taylor's law induced by synchronization of periodic and chaotic oscillators
著者名: Yuzuru Mitsui* and Hiroshi Kori
DOI: 10.1103/PhysRevLett.134.167202
URL: https://doi.org/10.1103/PhysRevLett.134.167202
研究助成
本研究は、科研費「群集生態学と数理疫学におけるダイナミクスごとの最適なネットワーク構造の探索(課題番号:23KJ0830)」、「振動子ネットワークの機能的構造の解明(課題番号:21K12056)」、および東京大学「未来社会協創」国際卓越大学院(WINGS CFS)の支援により実施されました。
用語解説
(注1)べき乗則
ある変数yが別の変数xのべき乗に比例する、つまりy=axbの関係があるときxとyの間にべき乗則が成立しているという。
(注2)同期現象
複数の時系列データの増減タイミングが一致することを同期現象と呼ぶ。
(注3)指数
y=axbの関係があるとき、bをべき乗則の指数という。
(注4)微分方程式
物事の時間変化を表すことができる方程式。物理学の分野でよく用いられる。
関連研究室